[2020년 1학기] 데이터 정보처리 입문 - 출석 대체 과제물 (30/30)

-목차-

1.     교재 1장 내용 – 연도별 출생성비

     (1)    출생성비, 합계출산율이 무엇을 의미하는지 조사하여 정리하시오.

     (2)    1990년부터 2018년까지의 연도별 전국 총출생성비를 시계열도표로 나타내고 전체적인 경향을 설명하시오.

     (3)    1990년부터 2018년까지의 연도별 서울과 부산의 총출생성비를 하나의 시계열도표에 나타내고 비교하여 설명하시오.

     (4)    1993년부터 2018년까지의 연도별 전국 합계출산율을 시계열도표로 나타내고 전체적인 경향을 설명하시오.

2.     교재 3장 내용 – 통계학 개론 점수 자료

     (1)    평균, 중앙값, 표본분산, 표본표준편차, 변동계수를 구하여 분포의 특징을 설명하시오.

     (2)    줄기-잎 그림, 히스토그램, 상자그림을 그리고 분포의 특징을 설명하시오.

3.     교재 4장 연습문제 1번

---

1.   교재 1장 내용 – 연도별 출생 성비

 

(1)    출생성비, 합계출산율이 무엇을 의미하는지 조사하여 정리하시오.

출생성비는 출생한 남아에 대한 여아의 비율로 보통 여아의 비율을 100으로 기준 잡았을 때의 남아의 수를 나타낸다. 출생성비는 부모의 연령, 계절, 지역, 직업, 인종 등 여러가지 조건에 따라서 큰 변동을 보인다.[1]

합계출산율은 여성 1명이 평생 동안 낳을 수 있는 평균 자녀 수이다. 국가별 출산력 수준을 비교하는 주요 지표로 이용되는데, 2가지 방법으로 산출된다. 먼저 일반적으로는 연령별 출산율의 합계를 해당 연령 수로 나누어 연령별 출산율을 산출한 다음 이렇게 계산한 각 연령별 출산율을 모두 더하면 합계출산율이 된다. 다른 하나는 5세 계급으로 계산된 연령별 출산율에 5를 곱하는 방식이다. 이 경우 전체 여성수는 미혼·기혼을 구별하지 않기 때문에 한국과 같이 혼인이 출산의 전제조건으로 작용하는 국가에서는 미혼 여성이 늘어날수록 출산율이 떨어진다.[2]

 

(2)    1990년부터 2018년까지의 연도별 전국 총출생성비를 시계열도표로 나타내고 전체적인 경향을 설명하시오.

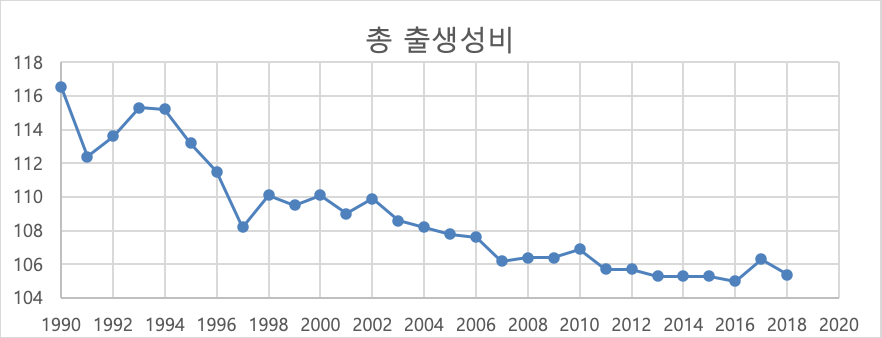
1990년 최고치 이후 1991년 4p 소폭 하락하였으나, 1993까지 115p경신 후 1997년 첫 100p대 경신 되고 1998 110p로 다시 상승하였으나 2000년대 이후 꾸준히 소폭 하락 되고있다.

2006년 이후 2p대 등락을 거듭하고 있는 중이다.

 

(3)    1990년부터 2018년까지의 연도별 서울과 부산의 총출생성비를 하나의 시계열 도표에 나타내고 배교하여 설명하시오.

1990년 부산 118, 서울 113p대로 시작하여 1991년 동반 하락 후 1993년 다시 1990년수치까지 반등하였고, 1994년 최고점을 찍은 이후 1997년까지 하락되는 추세다.

1990년 서울, 부산은 5p이상 차이가 났었으나 1997년까지 동반 하락을 하면서 4.5p까지 차이가 좁혀지더니 2002년 서울이 부산의 출생성비를 역전하는 현상이 발생한다.

2003년 부산이 다시 109p 서울 106p를 기록하며 재 역전이 되었으나 그 이후 2018년까지 104~108p까지 서로 엎치락 뒤치락 하는 추세다.

 

(4)    1993년부터 2018년까지의 연도별 전국 합계출산율을 시계열도표로 나타내고 전체적인 경향을 설명하시오.

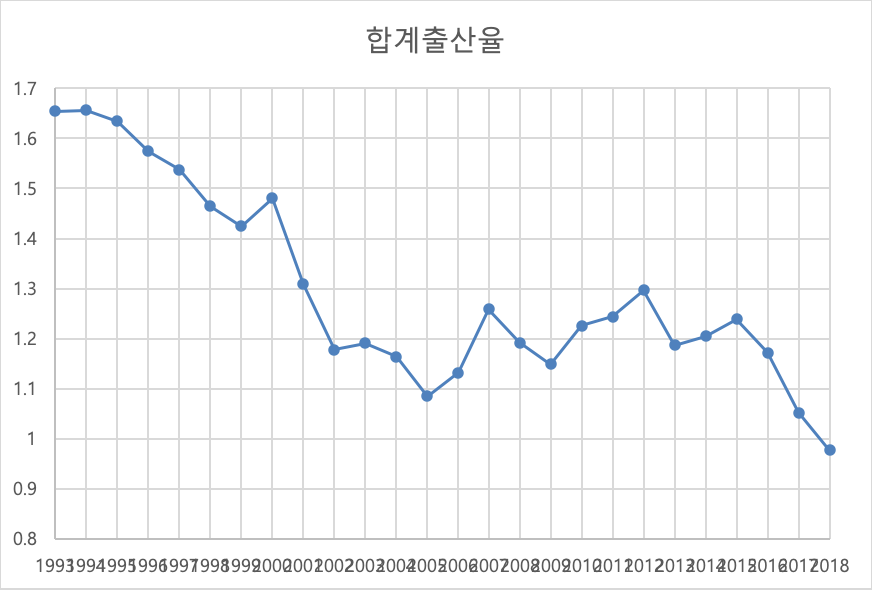
 1993년 합계출산율 1.6p로 시작하여 1995년까지 1.6p 소폭 등락하였으나 1995년 1.5p대까지 하락한 이후 별다른 상승세 없이 꾸준히 하락했다.

1999년 1.425p까지 떨어진 이후 2000년 1.48p까지 상승하였으나, 이후 2005년 1.085까지 하락했다.

2005년 이후 2016년까지 1.1~1.2p 등락폭을 반복하다 2017년 1.052p를 기록한 이후 2018년 첫 0.977p까지 떨어진 상태다.

 

 

2.   교재 3장 내용 – 통계학 개론 점수 자료

 

(1)    평균, 중앙값, 표본분산, 표본표준편차, 변동계수를 구하여 분포의 특징을 설명하시오

총 개수 65개로 이루어진score.txt는 최솟값 10, 최댓값 99이며, 각 값마다 변동계수는 2.35정도로 나타난다. 평균 값과 중앙값의 차이는 0.554로 확인 된다.

 

(2)    줄기-잎 그림, 히스토그램, 상자그림을 그리고 분포의 특징을 설명하시오.

1 | 00458

2 | 1333458889

3 | 0355789

4 | 11133456678

5 | 111222333444566788

6 | 14779

7 | 33478

8 | 29

9 | 09

줄기-잎 그림은 변수의 값을 자리수에 의거하여 나누어서 앞자리는 줄기로 하고, 뒷자리는 잎이라 하여 이를 그림으로 제시한 도수분포이다. 예를 들면, 어떤 변수의 값이 {12, 17, 22, 23, 25, 27, 31, 35, 38}이라면 10자리는 줄기이고 1자리는 잎으로서 다음과 같이 제시된다.[3]

 

히스토그램은 측정값이 존재하는 범위를 몇 개의 구간(급)으로 나눈 경우, 각 구간을 밑변으로 하고 그 구간에 속하는 측정값의 출현 도수에 비례하는 면적을 갖는 기둥(직사각형)으로 배열한 그림. 예를 들면 그림 Ⅰ은 섬유 제품 수분의 히스토그램으로, 표와 같은 도수표를 그림으로 나타낸 것이다. 히스토그램에 있어서 구간의 폭이 한정없이 작아지고 구간의 수를 한없이 늘릴 때, 각 구간의 도수의 값을 이으면 그림 Ⅱ와 같은 곡선을 얻을 수 있다. 이것을 분포 곡선이라 한다.[4]

 

상자그림은 평균이나 표준편차와 같이 전통적으로 많이 사용되는 측도는 자료에 이상점이 있는 경우 심하게 왜곡될 가능성이 있다. 따라서 자료에 이상점이 있는지를 확인할 필요가 있다. 상자그림은 자료에 이상점이 포함되어 있는지를 쉽게 판단할 수 있게 한다.[5]

 

해당 score.txt는 50대가 18개로 가장 많으며, 80,90대가 2개로 가장 적은 수로 분포되고 있는 상태다.

단일 개수로 가장 많은 개수를 차지하고 있는 값은 23,28,41,51,52,53,54로 각 3개씩 분포되어 있다.

---

[1] [출생성비], 네이버 지식백과, https://terms.naver.com/entry.nhn?docId=1595991&cid=50309&categoryId=50309

[2] [합계출산율], 네이버 지식백과, https://terms.naver.com/entry.nhn?docId=1221562&cid=40942&categoryId=31609

[3] [줄기-잎 그림], 네이버 지식백과, https://terms.naver.com/entry.nhn?docId=1924466&cid=42125&categoryId=42125

[4] [히스토그램], 네이버 지식백과, https://terms.naver.com/entry.nhn?docId=2324100&cid=60227&categoryId=60227

[5] [상자그림], 네이버 지식백과, https://terms.naver.com/entry.nhn?docId=5669260&cid=60207&categoryId=60207